Intro to Differentiable Programming
DeepLearning classifier, LSTM, YOLO detector, Variational AutoEncoder, GAN – are these guys truly architectures in sense meta-programs or just wise implementations of ideas on how to solve particular optimization problems? Are machine learning engineers actually developers of decision systems or just operators of GPU-enabled computers with a predefined parameterized optimization program? Differentiable Programming can answer these and some other questions like to explain the model and to stop heat on our planet with brute-force end-to-end DNNs. Data Scientists already do a lot of custom programming to clean, filter and normalize data before passing it into a standard neural network block or to stack models for a better result. Now it is time to do custom programming after the standard NN block and this programming has to be differentiable.
Idea
Let’s consider handwritten character recognition using MNIST (EMNIST). The classical approach is to label thousands of samples and pass them through the convolutional or dense neural network. The result will be some model that can predict a letter. This supervised approach requires a lot of data labeled (there are semisupervised methods like Active Learning on MNIST – Saving on Labeling hat can reduce the labeling efforts), and it creates a model that cannot explain data itself and the results as well. It makes sense only for the same distributed data to be recognized in the same way.
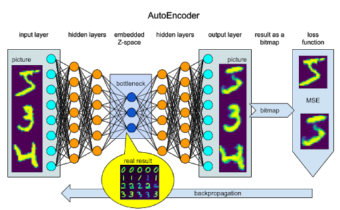
If we are brave enough to leave the safe harbor of supervised learning and use AutoEncoder to learn the embedded space using self-regression, we will find us not labeling data, but examining the Z-space for hidden features and insights. And the true result of this process is not a reproduced image, but learned embeddings that can be clustered and used for recognition, feature explanation, and manipulation. But we still cannot use the bottleneck of the AutoEncoder to connect it to a data transforming pipeline, as the learned features can be a combination of the line thickness and angle. And every time we retrain the model we will need to reconnect to different neurons in the bottleneck z-space.
What if to ask the neural network block to produce something useful from the beginning, like take a marker and draw the sign? This will be more like human beings are learning. We can interpret the DNN output as a list of points to draw with different marker sizes (pressure) and color intensity or even use the output as a single gesture that has to draw the handwritten sign. In this case, we will interpret the output as a set of velocity records (as first derivatives of positions).
In order to make these marker commands to produce an output that can be fully differentiable and, accordingly, transparent for backpropagation, we need to use the DiffProg approach. Classical programming tends to use too much “digital” operators that cannot pass gradient through them, like the step function cannot serve to adjust the initial parameters and we need to use sigmoid instead:
The same way we can use a Gaussian curve to emulate marker points, just need to present it in 2D space:
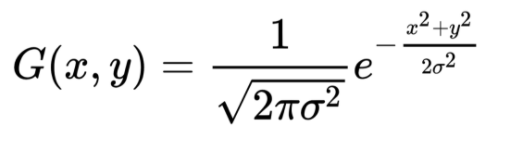
Here ? can be used as an inverse marker size, x and y are coordinates of the marker point and the color intensity can be driven by an additional amplifier coefficient:
In order to combine multiple marker points together, we can use the max function. And then the generated picture can be passed to the loss function – the same MSE:
As an actual result we will receive a model that can decompose image information in space and time(!), creating a program that will draw the requested sign in a single movement of, let’s say, robotic arm.
Implementation
We will not focus on the details of the Neural Network block as the article is about the concept of DiffProg. We just use some DNN with dense layers that act as a statistical estimator. The details of the implementation can be found in the notebooks that are listed in the References section. Let’s focus on the specifics of the TensorFlow implementation.
Static points
After loading MNIST data we create the model. Here we start with some parameters. The varcoef param is needed to translate size of marker in pixels to variance in the formula.
We use input data points as ground true:
The Neural Network serves to translate 728 MNIST pixels into 10 marker points. Each has vertical and horizontal position and size. We use sigmoid function for the activation of all the three point parameters. This is simplified variant and the results should not surprise us.
Here the DiffProg part starts – we need to put Gaussian formula into vectorized form and broadcast over batch size, 10 marker points and two dimensions of the picture. For this purpose we need to prepare GRAD_* as ?, MEAN_* as ? and VAR2 as 2?2 in the formula:
As result, we will have the MARKER tensor with shape: [batch size, points, vertical, horizontal].
The head part is pretty classical, except the fact that we will use max function for joining marker points in one glyph:
After training for 10 epochs the accuracy metric will be around 97% for both training and test datasets.
Training dataset pictures reproduced:
Test dataset pictures reproduced:

Visualization of the training process:
Dynamic gesture
Now we will go from the set of static points to a line that can reproduce the glyph. For this purpose we will change the code slightly in order to calculate point position as integral of velocity, predicted by the NN.
We are increasing the number of points as now not all of them will be visible. We also need a parameter for the maximal size of steps between points.
Using more deep NN block and introducing color intensity as additional marker point param.
For velocity of the marker on each step we need now -1:1 output range, thus we will use tanh activation and multiply them on the step_size. To calculate final point position we will need a cumulative sum of all previous velocity values plus initial point (left middle).
Markers are calculated now with additional AMP tensor that represents color intensity for each point.
While training for 50 epochs we will achieve 98% accuracy for train and test datasets. These are reproduced glyphs by one gesture for the training dataset:

And the test dataset:

The training process visualization:
Results
As we already discussed the actual result is the ability to learn to draw symbol glyphs as a human does. These are pictures of gesture tracks with marker size and color. Please note that the color intensity is crucial to draw more complex symbols that require multiple lines.
If we experiment with the training multiple times, we will observe that the style will be different every time, depending on the random seed.
Let’s move to more practical results – how to do symbol classification using this new technique. First, let’s perform clustering for whole 728 pixels of MNIST data over the test data set. This will produce the following results:
We assign every cluster a dominant sample label and use it for classification errors and accuracy metrics. When we do the same clustering over velocity and color intensity of the learned inverse graphics commands space, we will have:
As we can see, the number of errors was decreased by more than two times. Accuracy raised over 81%. It means using this unsupervised learning we managed to understand the data better and to classify the 10 handwritten digits much better than a set of not connected points.
EMNIST test
A quick check on EMNIST dataset with the same amount of train/test data – 60K/10K.
Reproduced glyphs for the training data:

for the test data:

Training dynamics visualisation:
Conclusion and next steps
This was just an example of what is possible if we stop to simply reuse existing vanilla NN blocks and start to do something specific to the problem. End-to-end networks cannot work in an efficient way, as efficiency is an indication of Intelligence that cannot be Artificial. It is just an Intelligence that Data Scientist or future Differential Programming Developer can add to the solution. If we build the model in the same way as the world is built, we need to make everything connected, like a quantum field, and this connection is the ability to take derivatives. Multiple derivatives in one point give information about the whole universe. Next steps for this particular model may include:
- The differential programming models can be not stable due to multiple imbalanced losses. This must be treated by regularization and better initialization.
- In the model, we selected an initial point for the gesture, but we did not force to finish in the opposite side of the picture in order to make handwritten symbols connected in one word. Such modification can solve the problem of handwritten recognition on the word level.
- It would be better to inverse graphics by a solid line, but it will require an advanced mathematical model.
- Predicting a chain of commands requires better NN block, possibly a need to use special RNN block there.
References
Code and examples
https://github.com/andy-bosyi/articles/blob/master/DiffProg-MNIST-position.ipynb https://github.com/andy-bosyi/articles/blob/master/DiffProg-MNIST-velocity.ipynb https://github.com/andy-bosyi/articles/blob/master/DiffProg-EMNIST-velocity.ipynb
Articles about DiffProg
https://skymind.ai/wiki/differentiableprogramming https://fluxml.ai/2019/02/07/what-is-differentiable-programming.html Author: Andy Bosyi, CEO/Lead Data Scientist MindCraft Information Technology & Data Science