Fast Fourier Transform (FFT) in Digital Sound Processing
This is a primitive prototype of the natural ear. Why I came to it and how it can be better than the Fast Fourier Transform (FFT) in Digital Sound Processing (DSP) – that what the article is about

Some of the software development projects that I was related to used Fourier Transform for waveform analysis. The projects Included sound tone recognition for gun targets and DTMF signals. But before that, I was keen to get a “picture” of the human speech and music harmony. Recently I started an app that will play some instrument while I am playing a lead guitar. The problem was to teach the computer to listen to my tempo and keep the musical rhythm in order. To accomplish this I used Fourier Transformation for the first seconds of Pink Floyd composition “Marooned”. Then I compared the “picture” to the same composition performed by me and the results were poor until I selected FFT block size as much as 8192 to recognize notes at least to 6th octave.
This showed the first problem with Fourier Transform – for really good analysis you need to increase block size (on a number of frequency bins) and, as result, performance goes down, especially for real-time processing.
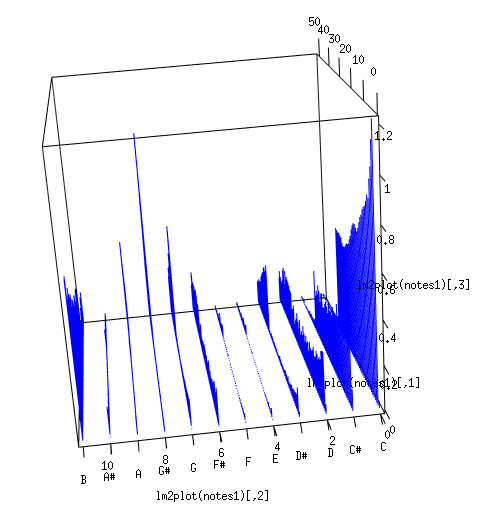
The second problem of Fourier Transform analysis for music – the same instrument depending on the timbre can generate the different set of overtones. These overtone frequencies analyzed by FFT created peaks that were irrelevant to what we actually hear. To generalize the result I summarized the frequency bins by twelve semitones. The picture was better, but now the very first note recognized as C, while it was B in fact:
This forced me to read more about the nature of sound, hearing and human ear. I thought that maybe the problem is the third problem with Fourier Transform – it is sensitive to the signal phase. The human ear does not recognize phase of individual harmonics, only frequencies.
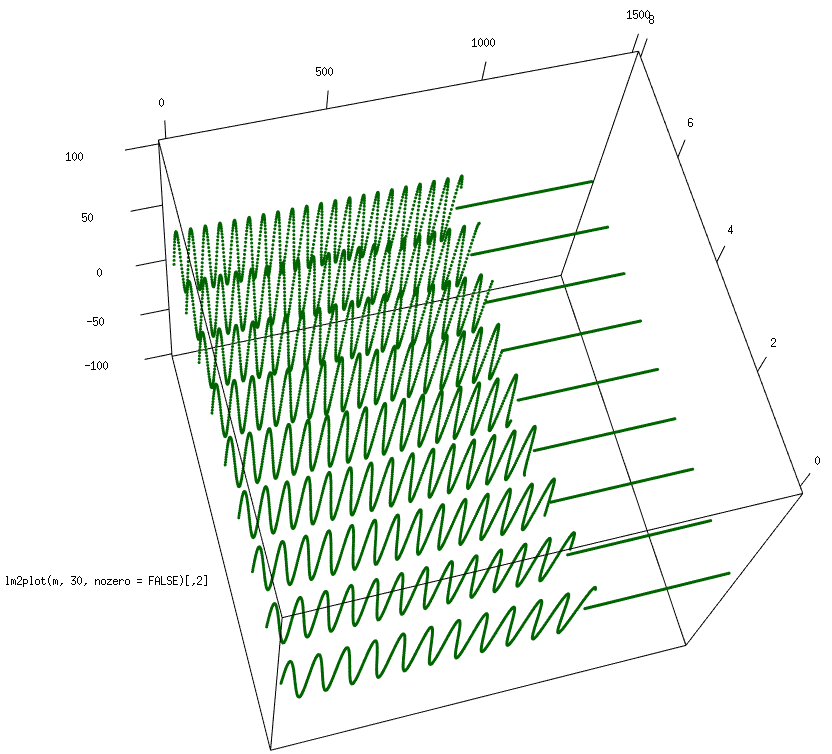
I created a model using R language (you can find the code at the end of the article) that generates input signals for a set of frequencies:
I created a model using R language (you can find the code at the end of the article) that generates input signals for a set of frequencies:
Then used some formulas I combined fifteen years ago ( the same experiment failed due to the poor PC performance) to create a model of a pendulum. The object can receive an incoming signal and oscillate if there is a frequency in the signal that is the same it’s
Frequency:The fading coefficient that does not depend on the auto-oscillation frequency of the pendulum:The position of the pendulum:Velocity and energy:This is a reaction of the pendulum on the same frequency signal:

green – input signal
blue – pendulum oscillation
red – pendulum energy
For the input signal that slightly differs from the frequency of the pendulum the amplitude and energy are significantly smaller than in the previous result:

Combined plot for nine different signals – the central one has been recognized:

After that, I built a set of pendulums for different frequencies to cover five octaves and twelve notes. This is resulting energy for 60 pendulums listening to the first chords of “Marooned”:

And as result, the main tone was detected correctly. I think that ability of the human ear to omit the phase information of the input signal is crucial for the music recognition. I used this model to create a C++ library named Cochlea to listen, detect and synchronize music in real-time. That will be described in next article.
R CODE
Also Read: Active Learning on MNIST – Saving on Labeling